Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Descriptive Statements:
- Use multiple representations (e.g., pictures, graphs, motion maps) to analyze the one-dimensional motion of a particle or an object.
- Solve problems involving constant acceleration.
- Apply properties of vectors to describe and analyze motion in two dimensions, including uniform circular motion and projectile motion.
- Solve problems involving motion in two dimensions, including uniform circular motion and projectile motion.
Sample Item:
A ball at rest on level ground is kicked into the air. The ball strikes the ground
4.00 s later at a horizontal distance of 40.0 m from where it was kicked. What is the
magnitude of the initial velocity of the ball?
- 10.0 m/ slash s
- 19.6 m/ slash s
- 22.0 m/ slash s
- 40.5 m/ slash s
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
C. This question requires the examinee to apply properties of vectors
to analyze projectile motion. Since the ball travels a horizontal distance of 40.0 m in
4.00 s, the horizontal component of its initial velocity is 10.0 m/ slash s. The ball is in
flight for a total of 4.00 s, so it reaches its maximum height in 2.00 s. Using the
equation v(t) = –9.8t + v0y and v(2.00) = 0.00 gives v0y = 19.6 m/sv left parenthesisnt right parenthesis equals negative 9.8t plus v subscript 0 subscript y and v left parenthesis 2.00 right parenthesis equals 0.00 gives v subscript 0 subscript y equals 19.6 m slash s. The magnitude of the initial velocity is therefore
v0 = 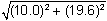 = 22.0 m/sv 0 equals square root left parenthesis 10.0 right parenthesis squared plus left parenthesis 19.6 right parenthesis squared equals 22.0 m slash s.
= 22.0 m/sv 0 equals square root left parenthesis 10.0 right parenthesis squared plus left parenthesis 19.6 right parenthesis squared equals 22.0 m slash s.
Descriptive Statements:
- Identify characteristics of Newton's laws in a variety of situations.
- Analyze free body diagrams.
- Use Newton's laws to solve problems involving force and motion, including problems involving gravitational, frictional, and elastic forces.
- Solve problems involving uniform circular motion, including satellite and planetary motion.
- Apply Newton's laws to solve problems involving systems of particles and the statics and dynamics of fluids.
Sample Item:
A rope with a tension of 10.0 N is attached to a 2.00 kg mass. The rope makes an
angle of 30.0° degrees with the horizontal.
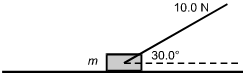
What is the normal force on the mass?
- 5.0 N
- 9.8 N
- 14.6 N
- 19.6 N
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
C. This question requires the examinee to solve problems involving
force and motion. There are three forces acting on the mass in the y-direction: the
gravitational force, the normal force, and the vertical component of the tension in the
string. The normal force is perpendicular to the surface of the mass and in the positive
y-direction. From Newton's second law, ∑F = masigma-summation F equals ma
applied in the y-direction, ∑Fy = 0 = –mg + N + T
sin 30°sigma-summation F subscript y equals 0 equals negative mg plis N plus T
sine 30 degrees. Using g = 9.80 m/s2g equals 9.80 m slash s squared, substituting the values given,
and solving for the normal force gives N = 14.6 NN equals 14.6 N.
Descriptive Statements:
- Apply principles of work, potential energy, kinetic energy, and power to solve problems.
- Apply the work-energy theorem to conservative and nonconservative systems.
- Analyze the relationships among force, impulse, and momentum.
- Solve problems involving elastic and inelastic collisions in one and two dimensions.
Sample Item:
A mass initially at rest at a height of 6r slides down a frictionless track and around
a circular loop of radius r.
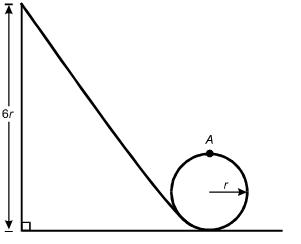
What is the speed of the mass at the top of the circular loop (point A)?
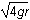 The square root of 4gr
The square root of 4gr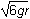 The square root of 6gr
The square root of 6gr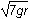 The square root of 7gr
The square root of 7gr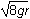 The square root of 8gr
The square root of 8gr
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
D. This question requires the examinee to apply the work-energy theorem to conservative systems. Since there are no frictional forces, the work done by friction is zero and the total mechanical energy is conserved. Therefore, mg(6r) = 1/2mv2 + mg(2r)mg left parenthesis 6r right parenthesis equals 1 half mv squared plus mg left parenthesis 2r right parenthesis. Solving this equation for v gives v = 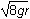 v gives v equals the square root of 8gr.
v gives v equals the square root of 8gr.
Descriptive Statements:
- Use graphs and trigonometric functions to analyze characteristics of simple harmonic motion, such as amplitude, restoring force, frequency, and period.
- Analyze the characteristics of kinetic and potential energy for an object undergoing simple harmonic motion.
- Solve problems in rotational kinematics.
- Solve static and dynamic problems involving torques and forces.
- Analyze systems involving rotational energy and angular momentum.
Sample Item:
A mass on a spring is displaced from equilibrium and released. The graph below shows
the velocity of the mass versus time.
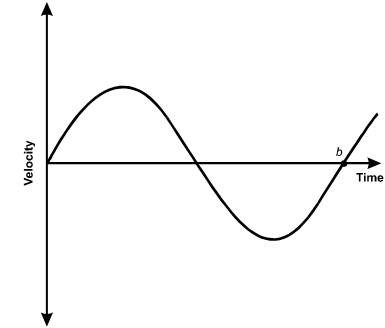
A sinusoid line starts at the origin with an upward slope. After the upper curve and the lower curve, the line passes through the horizontal axis at point b.
Which statement about the mass at time b must be true?
- It is located at its equilibrium position.
- Its potential energy is equal to zero.
- Its kinetic energy is at a maximum.
- Its acceleration is at a maximum.
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
D. This question requires the examinee to use graphs of trigonometric functions to analyze characteristics of simple harmonic motion. The graph shows the velocity of a mass oscillating on a spring. At point b the velocity is zero, so the mass is at one of its turning points and the displacement of the mass, x, is either A or −Anegative A, where A is the amplitude of motion. Since the slope of the line tangent to the curve at b is positive, the acceleration is positive, so x = –Ax equals negative A. Since F = ma = –kxF equals ma equals negative kx, the force, and therefore the acceleration, is maximum when x = –Ax equals negative A.