Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Descriptive Statements:
- Analyze phenomena related to static electricity, such as the behavior of electroscopes, induced molecular polarization, and charging by induction.
- Describe electric forces and electric fields for various simple charge distributions.
- Describe the motion of a charged particle in a constant electric field.
- Demonstrate knowledge of electric potential energy and potential difference.
Sample Item:
Three identical point charges are located on the vertices of an equilateral triangle
of side length s.
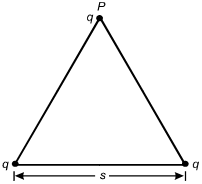
What is the vertical component of the electrostatic force on the charge located on
vertex P?
- kq2/s2 sin 30°kq squared over s squared sine 30 degrees
- kq2/s2 cos 30°kq squared over s squared cosine 30 degrees
- 2kq2/s2 sin 30°2kq squared over s squared sine 30 degrees
- 2kq2/s2 cos 30°2kq squared over s squared cosine 30 degrees
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
D. This question requires the examinee to describe an electric force
for a simple charge distribution. From Coulomb's law, the magnitude of the force on
q from the left-most charge on the base of the triangle is F =
kqq/s2,F equals
fraction kqq over s squared, and the component
in the vertical direction is kqq/s2
cos θ, where θ = 30°kqq over s squared
cosine theta, where theta equals 30 degrees. This force points in the positive y-direction.
The same applies for the force from the right-most charge. The net force is the
superposition of the two forces, which is F = 2kq2/s2 cos 30°F equals >2kq squared over s squared cosine 30 degrees.
Descriptive Statements:
- Demonstrate knowledge of the properties of magnets.
- Analyze the magnetic force on a moving charge in a magnetic field.
- Analyze the magnetic field for a current-carrying wire loop or solenoid.
- Apply Faraday's and Lenz's laws of induction to find the direction of an induced emf or current in a conducting loop.
- Describe the operation of devices such as electric motors, generators, and transformers.
Sample Item:
A wire that carries conventional current I in the direction shown is in a magnetic field
that points into the plane of the page.
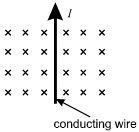
Which arrow shows the direction of the force on the wire?

Correct Response and Explanation (Show Correct ResponseHide Correct Response)
C. This question requires the examinee to analyze the magnetic force
on a moving charge in a magnetic field. The diagram shows a magnetic field that points
into the page. The wire carries conventional current, which implies positive charges
moving toward the top of the page. Since F = Iℓ
× B and ℓstart bold F end bold equals I samll l times start bold B end bold and small l represents
the direction of the conventional current I, the right-hand rule can be used to cross
v into Bstart bold v end bold into start bold B end bold. This shows that the force on the wire points to the left, as shown in response C.
Descriptive Statements:
- Demonstrate knowledge of electromotive force, electric current, resistance, and Ohm's law.
- Describe characteristics of parallel and series circuits.
- Solve problems using Kirchhoff's laws for circuits.
- Analyze an electric circuit or component in terms of energy or power.
Sample Item:
A resistor is connected in series across the terminals of an ideal battery of voltage
V. The resistor dissipates power W from the battery. A second,
identical resistor is connected in series with the first resistor. What is the total
power dissipated by the two resistors?
- W/2W over 2
- W
- 2W
- 4W
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
A. This question requires the examinee to analyze an electric circuit
in terms of energy or power. The power dissipated by the resistor in the circuit is
given by P = IV
= WP equals IV
equals W, where I is the current through
the resistor. When a second resistor is added to the circuit, the effective resistance
doubles. Since the voltage of the battery is the same, the current is
1/2I1 half I. Since there are
two identical resistors in the circuit, the voltage across each is
1/2V1 half V and the power dissipated
by each is P = 1/4WP equals 1 fourth W.
Therefore, the total power dissipated is P = 1/2WP equals 1 half W.